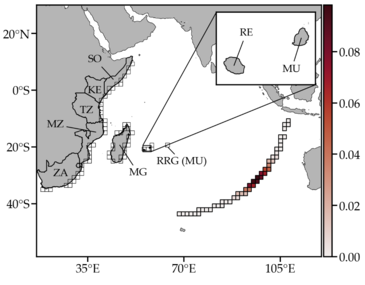
From Lagrangian datasets of surface buoys (such as the GDP and CARTHE drifters) or subsurface floats (such as RAFOS/SOFAR and Argos floats), probabilistic methods allows to combine the information contains in thousands of trajectories into a tool called the Transfer Operator.
The discrete version of this operator is the transition matrix P and each Pij coefficient represents the probability of moving from bin i to bin j during the fixed transition time T.
From an initial spatial distribution of a density f(x) (such as a passive tracer), a left multiplication (ft = f0P) by the transition matrix pushes forward the inital density to obtain its distribution at a latter time. See below the applications to the Pulley-Ridge reefs.
From the eigenspectrum (eigenvalues and eigenvectors) of the same transition matrix P, it is possible to extract the encoded region where trajectories converge and their respective basins of attraction. The right eigenvectors of P are the basins of attraction while the left eigenvectors are the attractors (or the almost-invariant region).
By combining almost-invariant region, it is possible to construct what we defined as a Lagrangian geography, fromed of weakly dynamically interacting provinces, which constrain the connectivity between distant locations within the Gulf of Mexico.
The surface Lagrangian geography highlights a main east–west division of the Gulf of Mexico and 5 coastal subdivisions,
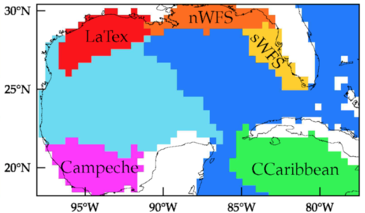
while the deep Lagrangian geography shows a similar east–west division with 4 subdivisions, including the WC region that contains a cyclone.