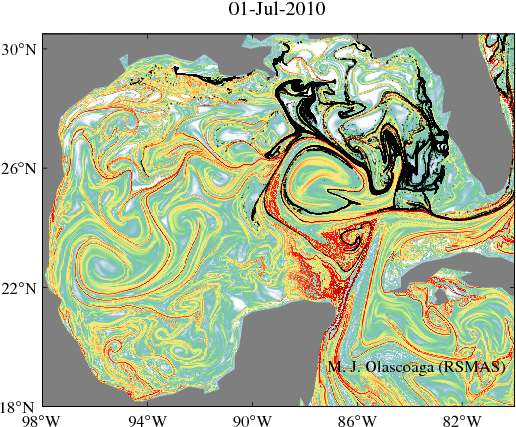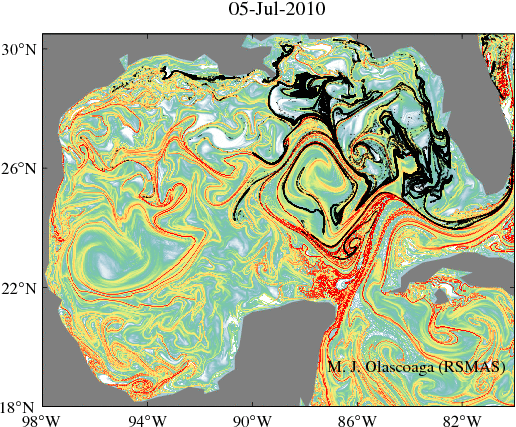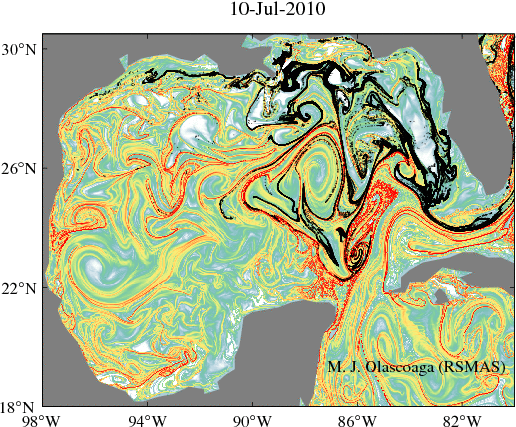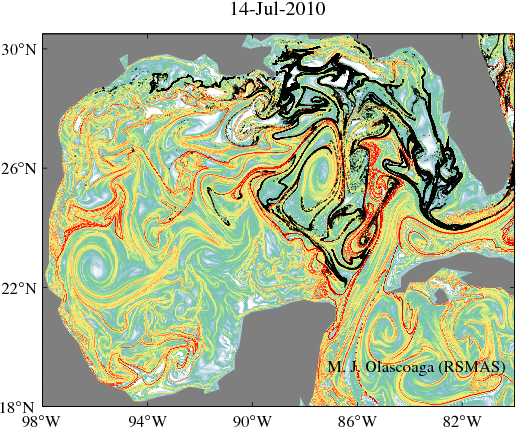
In a two-dimensional flows which depends arbitrarily on time and which is defined over a finite-time interval, LCS can be classified into three categories, each one with a distinguishing effect on transport. These three categories are: hyperbolic, elliptic, and parabolic. By bringing fluid into motion from regions with distinct flow characteristics, hyperbolic transport barriers are responsible for executing fluid exchange. Elliptic transport barriers are weakly-deforming closed material curves, i.e., they are analogous to KAM tori in temporally-periodic flows. As a result, elliptic transport barriers provide coherent eddies with the necessary confinement to trap and translate enclosed fluid. Finally, parabolic transport barriers are weakly-deforming, but open, material curves. Associated with jet streams, parabolic transport barriers prevent transport across their axes.
Our group has contributed to develop and apply the geodesic theory of LCS, which seek LCS as stationary curves of appropriate averaged objective (i.e., observer-independent) measures of fluid deformation. Recent applications of the Haller–Beron-Vera–Farazmand–Blazevski geodesic theory of LCS include efforts to explain transport of hydrocarbons in the Gulf of Mexico. We have also reported the occurrence in the ocean of chevron structures associated with zonal jets in Jupiter's weather layer that are characterized as shearless-parabolic LCS.




